From predictors and SHAKE toward unified integration scheme for molecular dynamics

Molecular dynamics (MD) simulations give us a substantially detailed insight into what is going on in a molecular system of interest. Throughout the years of their evolution, several MD algorithms have been developed. However, the initial abundant variability of integration methods for solving the underlying equations of motion has been narrowed to a very limited set of methods generally accepted as the best. Despite being appropriate in many applications, situations may occur in which alternative implementation could be advantageous. Therefore, the purpose of this work is to show an alternative universal way of MD algorithm construction based on predictors. The suggested unified integration scheme for MD includes a lot of variability that has once been lost.

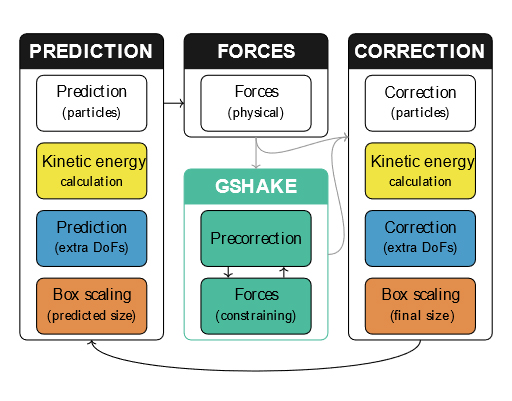
To formulate such a scheme, we adapted the traditional SHAKE method for treating rigid bonds to a predictor-corrector integration scheme and combined it with the existing time-reversible velocity predictor and box predictor. This new approach enables using both the time-honored Verlet method and the recently improved Gear methods. The resulting unified integration scheme was tested on two simple models and two MD systems: SPC/E water and ionic liquid (1-ethyl-3-methylimidazolium tetrafluoroborate). Trajectories in microcanonical, Nosé–Hoover canonical, and MTK isobaric ensembles were generated. The results for Verlet-based methods were in excellent agreement with those obtained using conventional integration methods. For particular tasks, the use of higher-order methods can be beneficial. Overall, in comparison with standard approaches, our universal scheme provides a significantly simpler route to devising new integrators and maintaining existing simulation software. Furthermore, our family of new integrators can be efficiently deployed in massively parallel MD software.

• J. Janek: From predictors and SHAKE toward unified integration scheme for molecular dynamics. J. Chem. Phys. 162, 084103, 2025. DOI