At the beginning of this year (2021) the team of Dr. Malijevsky from our institute in a collaboration with the University of Imperial College London published a theoretical work in the prestigious journal Physical Review Letters. By means of methods of statistical mechanics, the study describes the behavior of model fluids confined by a slit pore, whose walls are formed by periodically alternating stripes of different materials.
It is well known that solid surfaces which are corrugated or chemically heterogeneous, exhibit dramatically different or even qualitatively new wetting behavior compared to those which are perfectly smooth and homogenous. One of such phenomena is a hysteresis of a contact angle of a liquid drop on a rough or heterogeneous surface whose value may be smaller or larger than Young’s contact angle depending on whether the liquid is added to or removed from a drop. In particular, an effective (apparent) contact angle for chemically heterogeneous surfaces is given by Cassie’s law as a means of cosines of Young’s contact angles of the corresponding species of the composite.
Our study shows that for a sufficiently large (compared to the periodicity of the walls pattering) width L of the slit, the system exhibits – in a complete analogy with a homogenous case – capillary condensation at the pressure given rather accurately by a modified Kelvin equation, in which Young’s contact angle is replaced by Cassie’s effective angle. However, there exists a threshold value of the slit width L*, such that for L<L* the condensation occurs in two steps involving an intermediate bridging phase, in which case liquid bridges connect adjacent, more hydrophilic stripes (see the middle panel of the figure), before the system condenses globally. The two-phase transitions occur at pressures given by two Kelvin-like equations which contain different contact angles due to interfacial pinning, with one larger and one smaller than the Cassie effective angle in a strong analogy with the phenomenon of the contact angle hysteresis, which thus can be interpreted geometrically. We determine the triple point and predict two types of dispersion force-induced Derjaguin-like corrections due to mesoscopic volume reduction and the singular free-energy contribution from nanodroplets and bubbles. We test these predictions using a fully microscopic density functional model which confirms their validity even for molecularly narrow slits.
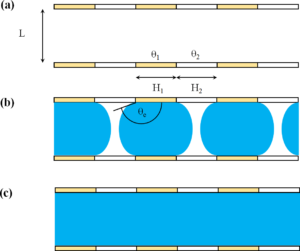
- Martin Láska, Andrew O. Parry, Alexandr Malijevský: Breaking Cassie’s Law for Condensation in a Nanopatterned Slit. Physical Review Letters 2021, 126(12), 125701 (5 pp). DOI: 10.1103/physrevlett.126.125701