Na začátku tohoto roku (2021) byla v prestižním fyzikálním časopise Physical Review Letters publikována teoretická práce týmu doc. Malijevského z našeho ústavu ve spolupráci s univerzitou Imperial College London. Práce popisuje metodami statistické mechaniky chování modelové tekutiny v rovinném póru, jehož stěny jsou tvořeny periodicky se střídajícími proužky dvou různých materiálů.
Je dobře známo, že povrchy pevných látek, které jsou zvrásněné či chemicky heterogenní, vykazují výrazně odlišné chování smáčivosti oproti perfektně hladkým a homogenním povrchům, a také kvalitativně nové jevy. Jedním z takových jevů je hystereze kontaktního úhlu makroskopické kapky na strukturovaném povrchu, který je buď větší či menší než odpovídající Youngův úhel (definovaný pro hladkou a homogenní stěnu) v závislosti na tom, zda objem kapky roste nebo klesá. Speciálně pro chemicky heterogenní povrchy zavádí Cassieho zákon efektivní kontaktní úhel jako vážený průměr kosinů Youngových úhlů odpovídajících složek kompozitu.
Z publikované studie vyplývá, že pro dostatečné velkou (oproti periodicitě vzorkování) šířku póru L, dochází v systému — v naprosté analogii k homogennímu případu — ke kapilární kondenzaci, a to za tlaku daném s dobrou přesností modifikovanou Kelvinovou rovnicí, v níž místo Youngova kontaktního úhlu vystupuje Cassieho efektivní úhel. Existuje nicméně taková mezní šířka L*, že pro L<L* dochází ke kondenzaci ve dvou krocích, během nichž dojde nejprve k vytvoření kapalných filmů (mostů) spojujících pouze protilehlé hydrofilnější části stěn (viz prostřední panel obrázku) a teprve potom ke globální kondenzaci. K těmto dvěma fázovým přechodům dochází za tlaků daných novými verzemi Kelvinovy rovnice, ve kterých vystupují tzv. mezní kontaktní úhly, z nichž jeden je větší a druhý menší než Cassieho efektivní úhel, se zjevnou analogií k jevu hystereze kontaktního úhlu, jemuž je tak dána geometrická interpretace. Dále jsme ukázali, že systém vykazuje trojný bod a určili jeho polohu. Výše zmíněné predikce jsme dále upřesnili zahrnutím mezoskopické Derjaguinovy korekce, která bere v potaz přítomnost mikroskopických kapiček a bublinek. Tyto analytické předpovědi jsme porovnali s numerickými výpočty založenými na mikroskopické teorii funkcionálu hustoty, a ověřili tak kvantitativní přesnost teorie, a to i pro pro šířky pórů na molekulárních škálách.
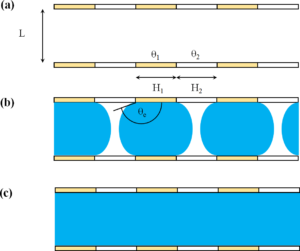
Obr. Schématická ilustrace tří možných fází uvnitř modelu periodicky vzorkovaného póru: (a) plynná, nízko-hustotní fáze, (b) fáze přemostění, (c) kapalná, vysoko-hustotní fáze.
- Martin Láska, Andrew O. Parry, Alexandr Malijevský: Breaking Cassie’s Law for Condensation in a Nanopatterned Slit. Physical Review Letters 2021, 126(12), 125701 (5 pp). DOI: 10.1103/physrevlett.126.125701