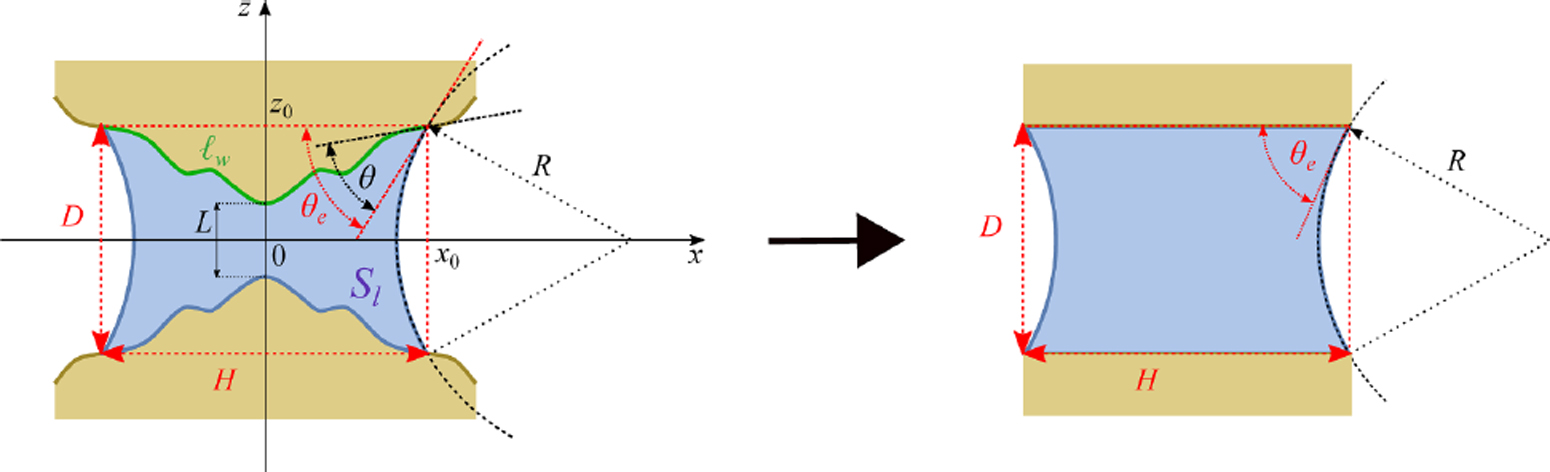
If two solid surfaces immersed in a fluid get sufficiently close together, a local condensation between them may occur. These so-called bridging transitions, referring to the formation of a liquid film connecting the surfaces, depend sensitively on their shape. The theoretical study led by Prof. Alexandr Malijevský and published in Physical Review E formulates general conditions for bridging transitions between a pair of surfaces of arbitrary shapes. We have shown that the problem can be solved effectively by an appropriate mapping of the system to a much simpler one formed by a pair of parallel plates leading to a newly generalized Kelvin equation (see Fig. 1). The equation was utilized to examine asymptotic behavior of bridging transitions and their relation to capillary condensation for a class of fundamental walls geometries. We have shown that the gradual flattening of the confining walls leads to a critical phenomenon characterized by a diverging growth of the bridging film. Associated geometry-dependent critical exponents were determined, and a covariance law revealing a relation between the geometric and Young’s contact angle for wedge-like structures was found. All the analytical predictions were confirmed numerically using appropriate molecular models.
Fig. 1. Bridging between a pair of walls of complex geometry (left) can be mapped to a system formed of planar walls of appropriate dimensions (right)
- Malijevský A.*, Pospíšil M.: Kelvin equation for bridging transitions. Physical Review E 2024, 109 (3 March), 034801. doi: 10.1103/PhysRevE.109.034801