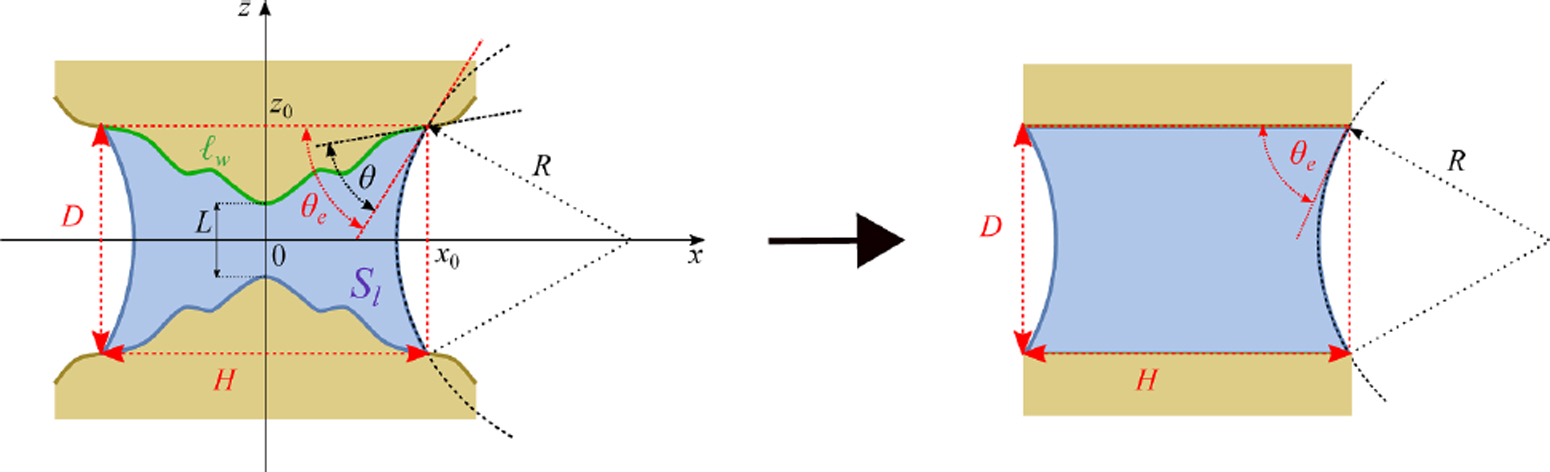
Pokud jsou dva pevné povrchy vnořené do tekutiny dostatečně blízko od sebe, může mezi nimi dojít k lokální kondenzaci. Tento fázový přechod přemostění, odpovídající formaci kapalného můstku spojujícího oba povrchy, závisí citlivě na tvaru těchto povrchů. Teoretická studie vedená prof. Alexandrem Malijevským a publikovaná v časopise Physical Review E ukázala, že vhodným zobrazením tohoto jevu na jednodušší model rovinného typu (viz obr. 1), lze odvodit obecnou podmínku pro kondenzaci mezi dvěma povrchy libovolných tvarů. Tento výsledek byl dále využit pro studium přemostění pro širokou třídu fundamentálních geometrií. Zde jsme ukázali, že existuje nový kritický jev odpovídající postupnému “narovnávaní“, kdy dochází k divergenci šířky kapalného můstku. Pro tento jev jsme odvodili kritické koeficienty, jejichž hodnoty závisí na geometrii systému a též odhalili kovariantní vztah mezi geometrickým a Youngovým úhlem pro případ povrchů tvořících klínovitou strukturu. Všechny tyto analytické predikce jsme potvrdili numericky pomocí vhodných molekulárních modelů.
Obr. 1. Fázový přechod přemostění mezi dvěma povrchy komplexní geometrie (vlevo) lze zobrazit na systém tvořený rovinnými stěnami odpovídajících rozměrů (vpravo)
- Malijevský A.*, Pospíšil M.: Kelvin equation for bridging transitions. Physical Review E 2024, 109 (3 March), 034801. doi: 10.1103/PhysRevE.109.034801