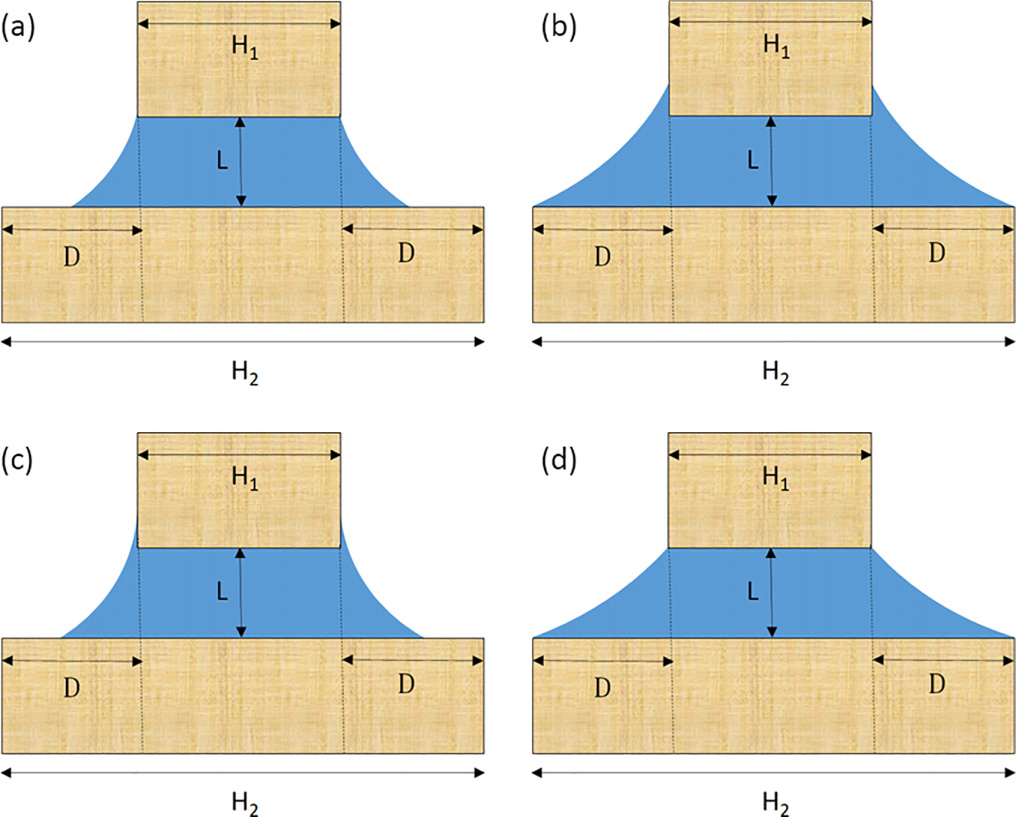
In an article published in Physical Review E (American Physical Society), Prof. Alexandr Malijevský from the Research Group of Molecular and Mesoscopic Modelling presents a new theory of capillary condensation between parallel walls of unequal length, i.e., in geometries that more closely reflect real micro- and nanostructures than the idealized case of infinitely long slits. The study demonstrates that the finite length of the confining walls and the presence of edges play a crucial role in determining how a liquid phase forms under confinement. By introducing the concept of the edge contact angle, the author identifies four qualitatively distinct condensation states, differing in whether the menisci are pinned to the upper wall, the lower wall, to both walls, or to neither of them.
For each of these states, Kelvin-like relations are derived that specify the conditions for the onset of condensation as functions of the system geometry and wall wettability. The resulting phase diagrams reveal two key organizing mechanisms: (i) a geometric separatrix at the wall-length ratio D = L, which divides distinct condensation regimes, and (ii) the wedge-filling transition at the contact angle θ = π/4. Below this threshold, all four types of condensation are possible, whereas above it only two remain. The results are important not only for the fundamental physics of interfaces, but also for applications in microfluidics, porous materials, and nanoelectromechanical systems, where capillary effects and the configuration of menisci often play a decisive role.
Schematic representation of the possible condensation states in an asymmetric slit formed by parallel walls of unequal length
- Malijevský A.: Capillary condensation between parallel walls of unequal length. Physical Review E. 2025, 112, 065502. doi.org/10.1103/zwzc-2z38