V článku publikovaném v časopise Physical Review E (American Physical Society) představuje prof. Alexandr Malijevský z Výzkumné skupiny molekulárního a mesoskopického modelování novou teorii kapilární kondenzace mezi rovnoběžnými stěnami nestejných délek, tedy v geometriích, které lépe odpovídají reálným mikro- a nanostrukturám, než idealizované nekonečné štěrbiny. Studie ukazuje, že konečná délka stěn a přítomnost hran zásadně ovlivňují způsob, jakým se v omezeném prostoru vytváří kapalná fáze. Zavedením pojmu hranového kontaktního úhlu autor identifikuje čtyři kvalitativně odlišné kondenzační stavy, lišící se tím, zda jsou menisky připnuty k horní či dolní stěně, oběma stěnám, nebo nejsou připnuty vůbec.
Pro každý z těchto stavů jsou odvozeny Kelvinovy rovnice, které určují podmínky vzniku kondenzace v závislosti na geometrii systému a smáčivosti stěn. Výsledné fázové diagramy odhalují dva zásadní organizační mechanismy: (i) geometrický separátor při poměru délek stěn D = L, který rozděluje kondenzační režimy, a (ii) mez fázového přechodu “wedge filling” při kontaktním úhlu θ = π/4; pod touto mezí jsou možné všechny čtyři typy kondenzace, zatímco nad ní zůstávají možné pouze dva. Získané výsledky mají význam nejen z hlediska fundamentální fyziky fázového rozhraní, ale i pro aplikace v mikrofluidice, porézních materiálech a nanoelektromechanických systémech, kde kapilární efekty a uspořádání menisků hrají klíčovou roli.
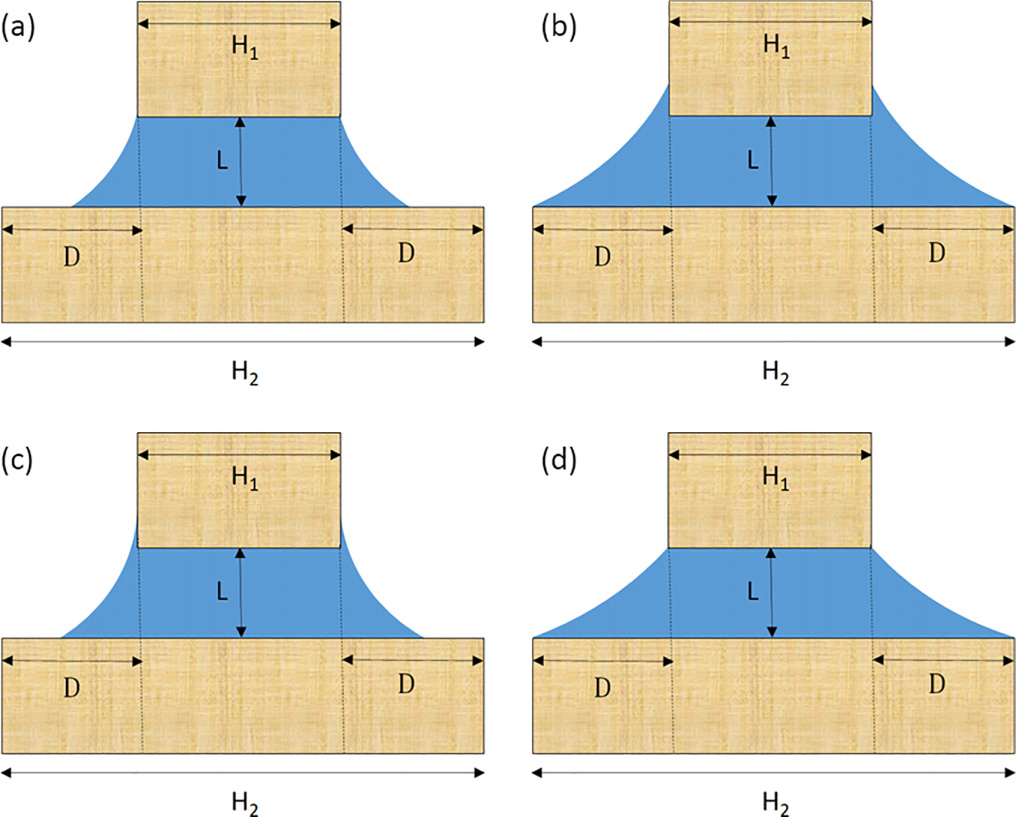
Schématické znázornění možných kondenzačních stavů v asymetrické štěrbině mezi rovnoběžnými stěnami nestejných délek
- Malijevský A: Capillary condensation between parallel walls of unequal length. Phys. Rev. E. 2025, 112, 065502. doi.org/10.1103/zwzc-2z38